逻辑回归常用于解决二分类问题,它将具有 $n$ 维特征的样本 $X$,经过线性加权后,通过 $sigmoid$ 函数转换得到一个概率值 $y$,预测时根据一个门限 $threshold$ (例如0.5)来划分类别,$y < threshold$ 为负类,$y \geq threshold$ 为正类。
感性认识
$sigmoid$ 函数 $\sigma (z) = \frac{1}{1+e^{-z}}$ 有如下图所示的漂亮S型曲线。
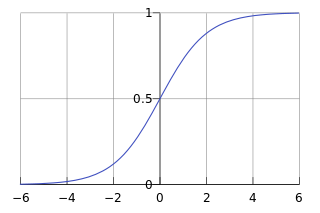
逻辑回归其实是在线性回归的基础上 $z = \sum_{i=1}^{n} {w_ix_i}$ ,借助 $sigmoid$ 函数将预测值压缩到0-1之间,实际上它是一种线性模型。其决策边界并不是上图中的S型曲线,而是一条直线或平面,如下图所示。
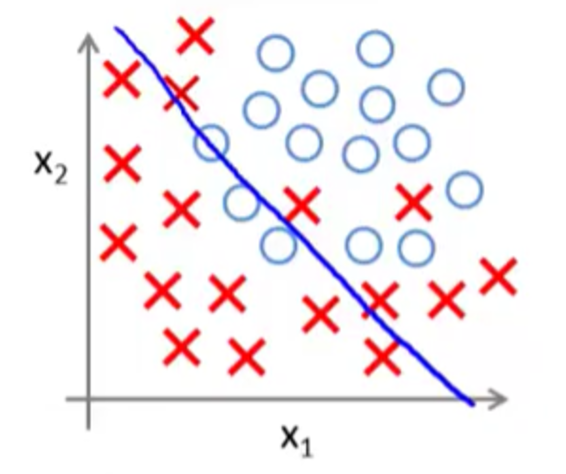
基本套路
机器学习问题,无外乎三点:模型,代价函数,优化算法。首先找到一个模型用于预测未知世界,然后针对该模型确定代价函数,以度量预测错误的程度,最后使用优化算法在已有的样本数据上不断地优化模型参数,来最小化代价函数。通常来说,用的最多的优化算法主要是梯度下降或拟牛顿法,计算过程都需要计算参数梯度值,下面仅从模型、代价函数以及参数梯度来描述一种机器学习算法。
基本模型:
$$ h_ \theta(X) = \frac {1} {1 + e^{-\theta^T X}} $$
$\theta$ 为模型参数,$X$ 为表示样本特征,它们均为 $n$ 维向量。
代价函数:
$$
J(\theta) = - \frac {1} {m} \sum_{i=1}^m \left( y^{(i)} logh_\theta(X^{(i)}) + (1-y^{(i)})(1-logh_\theta(X^{(i)}) \right)
$$
上述公式也称之为交叉熵,$m$ 为样本个数,$(X^{(i)}, y^{(i)})$ 为第 $i$ 个样本。
参数梯度:
$$
\bigtriangledown_{\theta_j} J(\theta) = \frac {1} {m} \sum_{i=1}^m \left[ \left( y^{(i)} - h_\theta(X^{(i)}) \right) X^{(i)}_j \right]
$$
$\theta_j$ 表示第 $j$ 个参数,$X^{(i)}_j$ 表示样本 $X^{(i)}$ 的第 $j$ 个特征值。
应用套路
在实际应用时,基于上述基本套路可能会有些小变化,下面还是从模型、代价函数以及参数梯度来描述。
通常来说在模型中会加个偏置项,模型变成如下形式:
$$ h_ {\theta,b}(X) = \frac {1} {1 + e^{-(\theta^T X + b)}} $$
为了防止过拟合,一般会在代价函数上增加正则项,常见的正则方法参考前面的文章“线性回归”。
加上正则项后,代价函数变成如下形式:
$$
\begin{split}
J(\theta, b) =& - \frac {1} {m} \sum_{i=1}^m \left( y^{(i)} log h_{\theta,b}(X^{(i)}) + (1-y^{(i)})(1-log h_{\theta,b}(X^{(i)}) \right) \\
&+ \frac {\lambda} {m} \left(\alpha \left \| \theta \right \| + \frac {1-\alpha} {2} {\left \| \theta \right \|}^2 \right)
\end{split}
$$
$\lambda$ 为正则项系数,$\alpha$ 为ElasticNet参数,他们都是可调整的超参数, 当 $\alpha = 0$,则为L2正则, 当 $\alpha = 1$,则为L1正则。L1正则项增加 $1/m$ 以及L2正则项增加 $1/2m$ 系数,仅仅是为了使求导后的形式规整一些。
由于 $sigmoid$ 函数在两端靠近极值点附近特别平缓,如果使用梯度下降优化算法,收敛非常慢,通常实际应用时,会使用拟牛顿法,它是沿着梯度下降最快的方向搜索,收敛相对较快,常见的拟牛顿法为L-BFGS和OWL-QN。L-BFGS只能处理可导的代价函数,由于L1正则项不可导,如果 $\alpha$ 不为0,那么不能使用L-BFGS,OWL-QN是基于L-BFGS算法的可用于求解L1正则的算法,所以当 $\alpha$ 不为0,可以使用OWL-QN。基于上述代价函数,下面仅列出包含L2正则项时的参数梯度:
$$
\begin{split}
\bigtriangledown_{\theta_j} J(\theta, b) &= \frac {1} {m} \sum_{i=1}^m \left( y^{(i)} - h_{\theta,b} (X^{(i)}) \right) X^{(i)}_j + \frac {\beta} {m} {\theta_j}^\ast \\
\bigtriangledown_b J(\theta, b) &= \frac {1} {m} \sum_{i=1}^m \left( y^{(i)} - h_{\theta,b} (X^{(i)}) \right)
\end{split}
$$
${\theta_j}^\ast$ 为上一次迭代得到的参数值。
Softmax
上述逻辑回归为二元逻辑回归,只能解决二分类问题,更一般地,可以推广到多元逻辑回归,用于解决多分类问题,一般将其称之为softmax,其模型、代价函数以及参数梯度描述如下。
基本模型
$$
H_\Theta(X) = \frac {1} {\sum_{j=1}^k exp(\Theta_j^T X)}
\begin{bmatrix}
exp(\Theta_1^T X)\\
exp(\Theta_2^T X)\\
…\\
exp(\Theta_k^T X)
\end{bmatrix}
$$
$H_ \Theta(X)$ 是一个 $k$ 维向量,$k$ 为类别的个数,对于一个实例 $X$ ,经过上述模型输出 $k$ 个概率值,表示预测不同类别的概率,不难看出,输出的 $k$ 个概率值之和为1。模型中的参数则可以抽象为如下矩阵形式:
$$ \Theta = \begin{bmatrix}-\Theta_1^T-\\ -\Theta_2^T-\\ \cdots \\ -\Theta_k^T-\end{bmatrix} $$ $\Theta_j$ 表示第 $j$ 个参数向量,如果参数中带有偏置项,那么总共有 $k \times (n+1)$ 个参数。
代价函数
$$ J(\Theta) = - \frac {1} {m} \left[\sum_{i=1}^m \sum_{j=1}^k 1 \left\{ y^{(i)} = j \right\} log \frac {exp(\Theta_j^T X)} {\sum_{l=1}^k exp(\Theta_l^T X)} \right] $$
$1 \left\{ y^{(i)} = j \right\}$ 为示性函数,表示 $y^{(i)} = j$ 为真时,其结果为1,否则为0.
参数梯度
$$
\begin{split}
& P\left( y^{(i)} = j \mid X^{(i)}, \Theta \right) = \frac {exp(\Theta_j^T X)} {\sum_{l=1}^k exp(\Theta_l^T X)} \\
& \bigtriangledown_{\Theta_j} J(\Theta) = \frac {1} {m} \sum_{i=1}^m \left[ \left( 1 \left\{ y^{(i)} = j \right\} - P\left( y^{(i)} = j \mid X^{(i)}, \Theta \right) \right ) X^{(i)} \right]
\end{split}
$$
$P\left( y^{(i)} = j \mid X^{(i)}, \Theta \right)$ 表示将 $X^{(i)}$ 预测为第 $j$ 类的概率,注意 $\bigtriangledown_ {\Theta_j} J(\Theta)$ 是一个向量。
总结
虽然逻辑回归是线性模型,看起来很简单,但是被应用到大量实际业务中,尤其在计算广告领域它一直是一颗闪耀的明珠,总结其优缺点如下:
- 优点:计算代价低,速度快,易于理解和实现。
- 缺点:容易欠拟合,分类的精度可能不高。
转载请注明出处,本文永久链接:https://sharkdtu.github.io/posts/ml-lr.html

