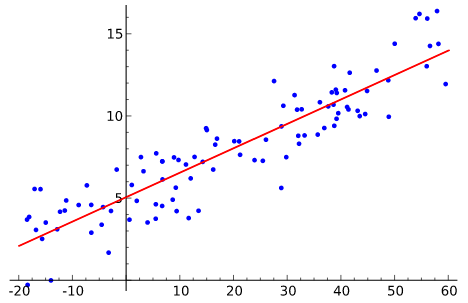
线性回归可以说是机器学习中最简单,最基础的机器学习算法,它是一种监督学习方法,可以被用来解决回归问题。它用一条直线(或者高维空间中的平面)来拟合训练数据,进而对未知数据进行预测。
基本套路
机器学习方法,无外乎三点:模型,代价函数,优化算法。首先找到一个模型用于预测未知世界,然后针对该模型确定代价函数,以度量预测错误的程度,最后使用优化算法在已有的样本数据上不断地优化模型参数,来最小化代价函数。通常来说,用的最多的优化算法主要是梯度下降或拟牛顿法(L-BFGS或OWL-QN),计算过程都需要计算参数梯度值,下面仅从模型、代价函数以及参数梯度来描述一种机器学习算法。
基本模型:
$$ \begin{split}
h_ \theta(X) &= \theta^T X \\
&= \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n
\end{split} $$
$X$ 为表示样本特征,为 $n$ 维向量,$\theta$ 为模型参数,为 $n+1$ 维向量,包括一个偏置 $\theta_0$
代价函数:
$$ J(\theta) = \frac {1} {2m} \sum_{i=1}^m \left ( y^{(i)}-h_\theta(X) \right ) ^2 $$
上述公式也称之为平方误差,$m$ 为样本个数,$(X^{(i)}, y^{(i)})$ 为第 $i$ 个样本。
参数梯度:
$$ \bigtriangledown_{\theta_j} J(\theta) = \frac {1} {m} \sum_{i=1}^m \left[\left ( y^{(i)} - h_ \theta(X^{(i)}) \right ) X^{(i)}_j \right] $$
$\theta_j$ 表示第 $j$ 个参数,$X^{(i)}_j$ 表示样本 $X^{(i)}$ 的第 $j$ 个特征值。
上述描述是按照常规的机器学习方法来描述线性回归,模型参数一般是通过梯度下降或拟牛顿法优化迭代得到,其实线性回归问题是可解的,只是在样本维度较大时很难求解才使用优化迭代的方法来逼近,如果样本维度并不是很大的情况下,是可以解方程一次性得到样本参数。
最小二乘:
$$ \theta = {\left( X^T X \right)} ^{-1} X^T y$$
注意这里 $X$ 为 $m \times n$ 矩阵,$n$ 为特征维度,$m$ 为样本个数; $y$ 为 $m \times 1$ 向量,表示每个样本的标签。
加权最小二乘:
$$ \theta = {\left( X^T W X \right)} ^{-1} X^T W y$$
$W$ 为 $m \times m$ 对角矩阵,对角线上的每个值表示对应样本实例的权重。
应用套路
在实际应用时,基于上述基本套路可能会有些小变化,下面首先还是从模型、代价函数以及参数梯度来描述。把基本套路中模型公式中的 $\theta_0$ 改成 $b$,表示截距项,模型变成如下形式:
$$
\begin{split}
h_{\theta,b}(X) &= \theta^T X + b \\
&= \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n + b
\end{split}
$$
正则化
为了防止过拟合,一般会在代价函数上增加正则项,常见的正则方法有:
- L1: $\lambda \left \| \theta \right \|$ , 也称之为套索回归(Lasso),可将参数稀疏化,但是不可导
- L2: $\frac {\lambda} {2} {\left \| \theta \right \|}^2$,也称之为岭回归(Ridge),可将参数均匀化,可导
- L1&L2: $\lambda \left(\alpha \left \| \theta \right \| + \frac {1-\alpha} {2} {\left \| \theta \right \|}^2 \right)$, 也称之为弹性网络(ElasticNet),具备L1&L2的双重特性
加上正则项后,代价函数变成如下形式:
$$
\begin{split}
J(\theta, b) =& \frac {1} {2m} \sum_{i=1}^m \left ( y^{(i)}-h_{\theta,b}(X) \right ) ^2 + \frac {\lambda} {m} \left(\alpha \left \| \theta \right \| + \frac {1-\alpha} {2} {\left \| \theta \right \|}^2 \right)
\end{split}
$$
$\lambda$ 为正则项系数,$\alpha$ 为ElasticNet参数,他们都是可调整的超参数, 当 $\alpha = 0$,则为L2正则, 当 $\alpha = 1$,则为L1正则。L1正则项增加 $1/m$ 以及L2正则项增加 $1/2m$ 系数,仅仅是为了使求导后的形式规整一些。
由于L1正则项不可导,如果 $\alpha$ 不为0,那么不能简单的套用梯度下降或L-BFGS,需要采用借助软阈值(Soft Thresholding)函数解决,如果是使用拟牛顿法,可以采用OWL-QN,它是基于L-BFGS算法的可用于求解L1正则的算法。基于上述代价函数,下面仅列出包含L2正则项时的参数梯度:
$$
\begin{split}
\bigtriangledown_{\theta_j} J(\theta, b) &= \frac {1} {m} \sum_{i=1}^m \left ( y^{(i)} - h_{\theta,b} (X^{(i)}) \right ) X^{(i)}_j + \frac {\lambda (1-\alpha)} {m} {\theta_j}^\ast \\
\bigtriangledown_b J(\theta, b) &= \frac {1} {m} \sum_{i=1}^m \left( y^{(i)} - h_{\theta,b} (X^{(i)}) \right)
\end{split}
$$
${\theta_j}^\ast$ 为上一次迭代得到的参数值。
实际上,使用L2正则,是将前面所述的最小二乘方程改成如下形式:
$$ \theta = {\left( X^T X + kI \right)}^{-1} X^T y$$
这样可以降低矩阵 $X^T X $ 奇异的可能,否则就不能求逆了。
标准化
一般来说,一个特征的值可能在区间 $(0, 1)$ 之间,另一特征的值可能在区间$(-\infty, \infty)$ ,这就是所谓的样本特征之间量纲不同,这样会导致优化迭代过程中的不稳定。当参数有不同初始值时,其收敛速度差异性较大,得到的结果可能也有较大的差异性,如下图所示,可以看到X和Y这两个变量的变化幅度不一致,如果直接使用梯度下降来优化迭代,那么量纲较大的特征信息量会被放大,量纲较小的特征信息量会被缩小。
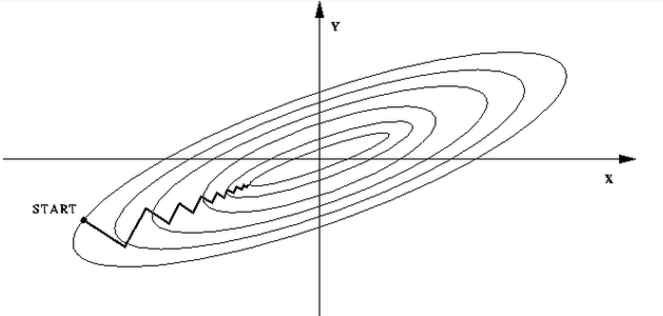
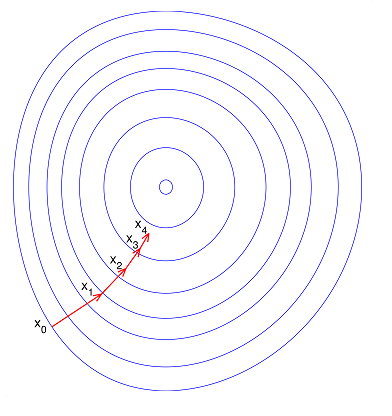
所以一般要对数据作无量纲化处理,通常会采用标准化方法 $(x-u)/\sigma$ ,得到如下数据分布,这样无论从哪个点开始,其迭代方向的抖动都不会太大,每个特征的信息也不至于被放大和缩小。
总结
虽然线性回归现在可能很少用于解决实际问题,但是因为其简单易懂,学习它有助于对机器学习有个入门级的初步掌握,了解机器学习的套路等。
转载请注明出处,本文永久链接:https://sharkdtu.github.io/posts/ml-linear-regression.html

