如今,协同过滤推荐(CollaboratIve Filtering)技术已广泛应用于各类推荐系统中,其通常分为两类,一种是基于用户的协同过滤算法(User-Based CF),它是根据用户对物品的历史评价数据(如,喜欢、点击、购买等),计算不同用户之间的相似度,在有相同喜好的用户间进行物品推荐,例如将跟我有相同电影爱好的人看过的电影推荐给我;另一种是基于物品的协同过滤算法(Item-Based CF),它是根据用户对物品的历史评价数据,计算物品之间的相似度,用户如果喜欢A物品,那么可以给用户推荐跟A物品相似的其他物品,例如如果我们在购物网站上买过尿片,第二天你再到购物网站上浏览时,可能会被推荐奶瓶。更多关于User-Based CF和Item-Based CF的阐述请参考文章。然而,在用户数量以及用户评分不足的情况下,上述两种方法就不是那么地好使了,近年来,基于模型的推荐算法ALS(交替最小二乘)在Netflix成功应用并取得显著效果提升,ALS使用机器学习算法建立用户和物品间的相互作用模型,进而去预测新项。
基本原理
用户对物品的打分行为可以表示成一个打分矩阵 $R$,例如下表所示:
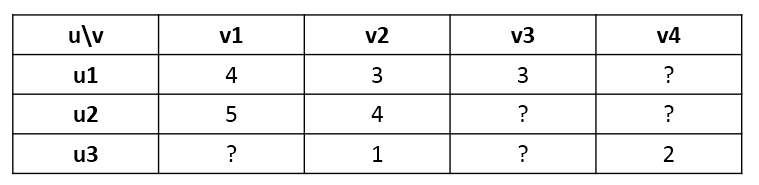
矩阵中的打分值 $r_{ij}$ 表示用户 $u_i$ 对物品 $v_j$ 的打分,其中”?”表示用户没有打分,这也就是要通过机器学习的方法去预测这个打分值,从而达到推荐的目的。
模型抽象
按照User-Based CF的思想,$R$ 的行向量对应每个用户 $u$ ,按照Item-Based CF的思想,$R$ 的列向量对应每个物品 $v$ 。ALS 的核心思想是,将用户和物品都投影到 $k$ 维空间,也就是说,假设有 $k$ 个隐含特征,至于 $k$ 个隐含特征具体指什么不用关心,将每个用户和物品都用 $k$ 维向量来表示,把它们之间的内积近似为打分值,这样就可以得到如下近似关系:
$$ R \approx U V^T $$
$R$ 为打分矩阵($m \times n$),$m$ 个用户,$n$ 个物品,$U$ 为用户对隐含特征的偏好矩阵($m \times k$),$V$ 为物品对隐含特征的偏好矩阵($n \times k$)。
上述模型的参数就是矩阵 $U$ 和 $V$,即求解出 $U$ 和 $V$ 我们就可以重现打分矩阵,填补原始打分矩阵中的缺失值”?”。
显示反馈代价函数
要求解上述模型中的 $U$ 和 $V$,那么就需要一个代价函数来衡量参数的拟合程度,如果有比较明确的显式反馈打分数据,那么可以比较重构出来的打分矩阵与实际打分矩阵,即得到重构误差,由于实际打分矩阵有很多缺失值,所以仅计算已知打分的重构误差,下面函数为显示反馈代价函数。
$$
J\left( U, V \right) = \sum_i \sum_j \left[ \left( r_{ij} - u_i v_j^T \right)^2 + \lambda \left( \|u_i\|^2 + \|v_j\|^2 \right) \right]
$$
$r_{ij}$ 为矩阵 $R$ 的第 $i$ 行第 $j$ 列,表示用户 $u_i$ 对物品 $v_j$ 的打分,$u_i$ 为矩阵 $U$ 的第 $i$ 行 $(1 \times k)$,$v_j^T$ 为矩阵 $V^T$ 的第 $j$ 列 $(k \times 1)$,$\lambda$ 为正则项系数。
隐式反馈代价函数
很多情况下,用户并没有明确反馈对物品的偏好,需要通过用户的相关行为来推测其对物品的偏好,例如,在视频推荐问题中,可能由于用户就懒得对其所看的视频进行反馈,通常是收集一些用户的行为数据,得到其对视频的偏好,例如观看时长等。通过这种方式得到的偏好值称之为隐式反馈值,即矩阵 $R$ 为隐式反馈矩阵,引入变量 $p_{ij}$ 表示用户 $u_i$ 对物品 $v_j$ 的置信度,如果隐式反馈值大于0,置信度为1,否则置信度为0。
$$ p_{ij} = \left\{\begin{matrix}1 \qquad r_{ij} > 0 & \\ 0 \qquad r_{ij} = 0 & \end{matrix}\right. $$
但是隐式反馈值为0并不能说明用户就完全不喜欢,用户对一个物品没有得到一个正的偏好可能源于多方面的原因,例如,用户可能不知道该物品的存在,另外,用户购买一个物品也并不一定是用户喜欢它,所以需要一个信任等级来显示用户偏爱某个物品,一般情况下,$r_{ij}$ 越大,越能暗示用户喜欢某个物品,因此,引入变量 $c_{ij}$,来衡量 $p_{ij}$ 的信任度。
$$ c_{ij} = 1 + \alpha r_{ij} $$
$\alpha$ 为置信度系数
那么,代价函数则变成如下形式:
$$
J\left( U, V \right) = \sum_i \sum_j \left[ c_{ij} \left( p_{ij} - u_i v_j^T \right)^2 + \lambda \left( \|u_i\|^2 + \|v_j\|^2 \right)\right]
$$
算法
无论是显示反馈代价函数还是隐式反馈代价函数,它们都不是凸的,变量互相耦合在一起,常规的梯度下降法可不好使了。但是如果先固定 $U$ 求解 $V$,再固定 $V$ 求解 $U$ ,如此迭代下去,问题就可以得到解决了。
$$ U^{(0)} \rightarrow V^{(1)} \rightarrow U^{(1)} \rightarrow V^{(2)} \rightarrow \cdots $$
那么固定一个变量求解另一个变量如何实现呢,梯度下降?虽然可以用梯度下降,但是需要迭代,计算起来相对较慢,试想想,固定 $U$ 求解 $V$,或者固定 $V$ 求解 $U$,其实是一个最小二乘问题,由于一般隐含特征个数 $k$ 取值不会特别大,可以将最小二乘转化为正规方程一次性求解,而不用像梯度下降一样需要迭代。如此交替地解最小二乘问题,所以得名交替最小二乘法ALS,下面是基于显示反馈和隐式反馈的最小二乘正规方程。
显示反馈
固定 $V$ 求解 $U$
$$ U ^T = \left( V^T V + \lambda I \right)^{-1} V^T R^T $$
更直观一点,每个用户向量的求解公式如下:
$$
u_i ^T = \left( V^T V + \lambda I \right)^{-1} V^T r_i^T
$$
$u_i^T$ 为矩阵 $U$ 的第 $i$ 行的转置($k \times 1$),$r_i^T$ 为矩阵 $R$ 的第 $i$ 行的转置($n \times 1$)。
固定 $U$ 求解 $V$
$$ V ^T = \left( U^T U + \lambda I \right)^{-1} U^T R $$
更直观一点,每个物品向量的求解公式如下:
$$
v_j ^T = \left( U^T U + \lambda I \right)^{-1} U^T r_j^T
$$
$v_j^T$ 为矩阵 $V^T$ 的第 $j$ 列($k \times 1$),$r_j^T$ 为矩阵 $R$ 的第 $j$ 列($m \times 1$)。
隐式反馈
固定 $V$ 求解 $U$
$$
U ^T = \left( V^T C_v V + \lambda I \right)^{-1} V^T C_v R^T
$$
更直观一点,每个用户向量的求解公式如下:
$$
u_i ^T = \left( V^T C_v V + \lambda I \right)^{-1} V^T C_v r_i^T
$$
$u_i^T$ 为矩阵 $U$ 的第 $i$ 行的转置($k \times 1$),$r_i^T$ 为矩阵 $R$ 的第 $i$ 行的转置($n \times 1$), $C_v$ 为对角矩阵($n \times n$)。
固定 $U$ 求解 $V$
$$
V ^T = \left( U^T C_u U + \lambda I \right)^{-1} U^T C_u R
$$
更直观一点,每个物品向量的求解公式如下:
$$
v_j ^T = \left( U^T C_u U + \lambda I \right)^{-1} U^T C_u r_j^T
$$
$v_j^T$ 为矩阵 $V^T$ 的第 $j$ 列($k \times 1$),$r_j^T$ 为矩阵 $R$ 的第 $j$ 列($m \times 1$),, $C_u$ 为对角矩阵($m \times m$)。
Spark 分布式实现
上述ALS算法虽然明朗了,但是要将其实现起来并不是信手拈来那么简单,尤其是数据量较大,需要使用分布式计算来实现,就更加不是那么地容易了。下面详细阐述Spark ML是如何完成ALS分布式实现的。为了更加直观的了解其分布式实现,下面用前面的打分矩阵作为例子,如下图所示。

由前面的原理介绍可知,按照显示反馈模型,固定 $U$ 求解 $V$,每个物品对隐含特征的偏好向量 $ v_j ^T$ 由以下公式得到:
$$ v_j ^T = \left( U^T U + \lambda I \right)^{-1} U^T r_j^T $$
计算时,只需要计算得到 $ U^T U + \lambda I $ 和 $U^T r_j^T$,再利用BLAS库即可解方程,初次迭代计算时,随机初始化矩阵 $U$,假设得到如下初始形式:
$$
U = \begin{bmatrix} -u_1- \\ -u_2- \\ -u_3- \end{bmatrix}
$$
假如求解 $v_1^T$,由于只有 $u_1$ 和 $u_2$ 对 $v_1$ 有打分,那么只需基于 $u_1$ 和 $u_2$ 来计算,根据相关线性代数知识就可以得到:
$$
\begin{split}
&U^T U = u_1^T u_1 + u_2^T u_2 \\
&U^T r_1^T = {\begin{bmatrix} u_1^T & u_2^T \end{bmatrix}} {\begin{bmatrix} 4 \\ 5 \end{bmatrix}} = 4u_1^T + 5u_2^T
\end{split}
$$
有了这个基本求解思路后,考虑 $u$ 的维度为 $k$,可以在单机上完成上述求解,那么就可以在不同task里完成不同物品 $v^T$ 的计算,实现分布式求解,由打分矩阵可以得到如下图所示的关系图。
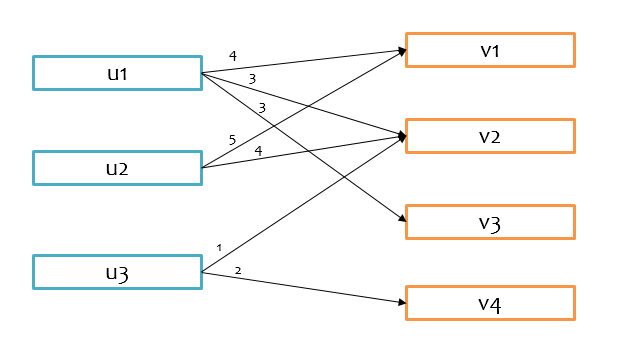
基于上述思路,就是要把有打分关联的 u 和 v 想办法放到同一个分区里,这样就可以在一个task里完成对 v 的求解,例如要求解 $v_1$,就必须把 $u_1$ 和 $u_2$ 以及其对应地打分放到同一个分区,才能利用上述公式求解。首先对uid和vid以Hash分区的方式分区,假设分区数均为2,那么分区后的大致情况如下图所示,$v_1$ 和 $v_3$ 在同一个分区中被求解,$v_2$ 和 $v_4$ 在同一个分区中被求解。
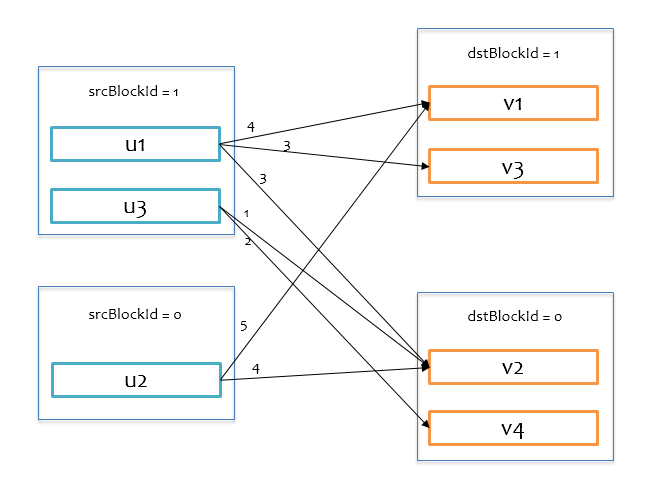
上面的图仅为感性认识图,实际上手头仅有的数据就是打分矩阵,可以通过一个RDD表示打分矩阵ratings,RDD中的每条记录为(uid, vid, rating)形式,由于是基于 $U$ 求解 $V$,把uid称之为srcId,vid称之为dstId,按照srcId和dstId的分区方式,将ratings重新分区,得到的RDD为blockRatings,其中的每条记录为((srcBlockId, dstBlockId), RatingBlock)形式,key为srcId和dstId对应的分区id组成的二元组,value(RatingBlock)包含一个三元组(srcIds, dstIds, ratings)。对于前面的打分关系,原始打分矩阵重新分区如下图所示。
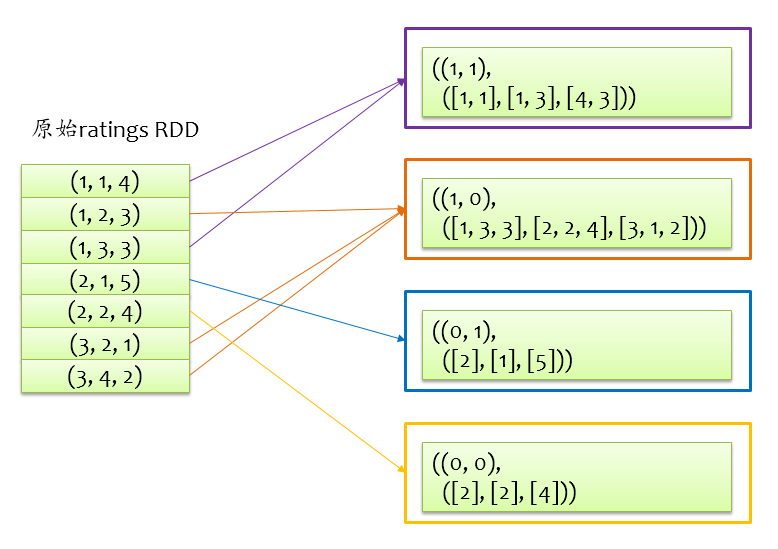
对于 u 来说,是要将自身信息发给不同的 v,对于 v 来说,是要接收来自不同 u 的信息,例如,要将 $u_1$ 发给 $v_1$、$v_2$、$v_3$ ,$v_1$ 要接收 $u_1$ 和 $u_2$。那么基于上述重新分区后的打分RDD,分别得到关于 u 的出口信息userOutBlocks,以及 v 的入口信息itemInBlocks,就可以通过join将两者联系起来计算了。由于后面基于 $V$ 求 $U$,也需要求解关于 u 的入口信息userInBlocks,以及 v 的出口信息itemOutBlocks,所以一次性计算好并缓存起来。以计算 u 的入口信息和出口信息为例,在前面得到的重新分区后的blockRatings基础上求解,如下图所示。
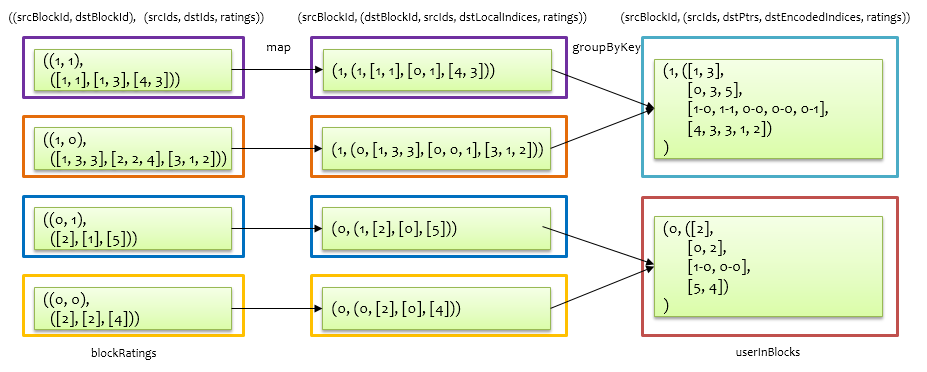
首先通过一个map操作,将记录形式((srcBlockId, dstBlockId), RatingBlock)转换为(srcBlockId, (dstBlockId, srcIds, dstLocalIndices, ratings)),其中dstLocalIndices为dstIds去重排序后,每个dstId的索引,最后根据srcBlockId做groupByKey,合并相同srcBlockId对应的value,合并过程中,对dstLocalIndices中的每个元素加上其对应的dstBlockId,这里做了一个优化,就是将localIndex和blockId用一个Int编码表示,同时采用类似CSC压缩编码的方式,进一步压缩srcIds和dstIds的对应关系。这样就按照 uid 进行分区后,得到 u 的入口信息,即将跟 u 关联的 v 绑定在一起了。基于该入口信息,可以进一步得到 u 的出口信息,如下图所示。
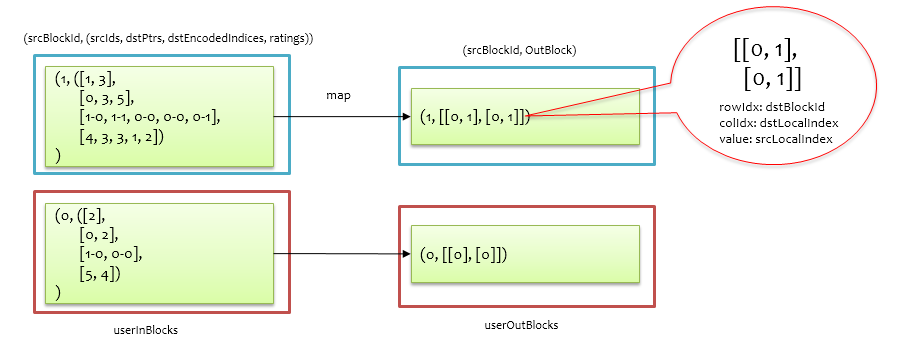
在userInBlocks基础上根据srcId和dstId的对应关系,通过map操作将(srcBlockId, (srcIds, dstPtrs, dstEncodedIndices, ratings))形式的记录转换为(srcBlockId, OutBlock)得到userOutBlocks,其中OutBlock是一个二维数组,有numDstBlock行,每一行为srcId所在srcBlockId中的索引,意为当前srcBlockId应该往每个dstBlockId发送哪些用户信息。
同理,在userInBlocks基础上初始化用户信息,得到userFactors,如下图所示,其中 $u_1$、$u_2$、$u_3$为随机初始化的向量($1 \times k$)。
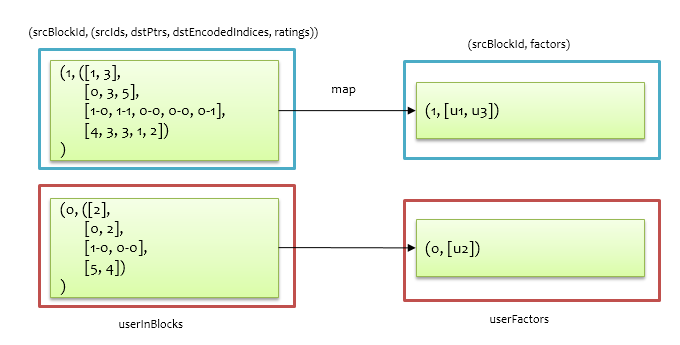
接着对userOutBlocks和userFactors做join 就可以模拟发送信息了,userOutBlocks中保存了应该往哪里发送的信息,userFactors中保存了用户信息,即一个掌握了方向,一个掌握了信息,如下图所示:
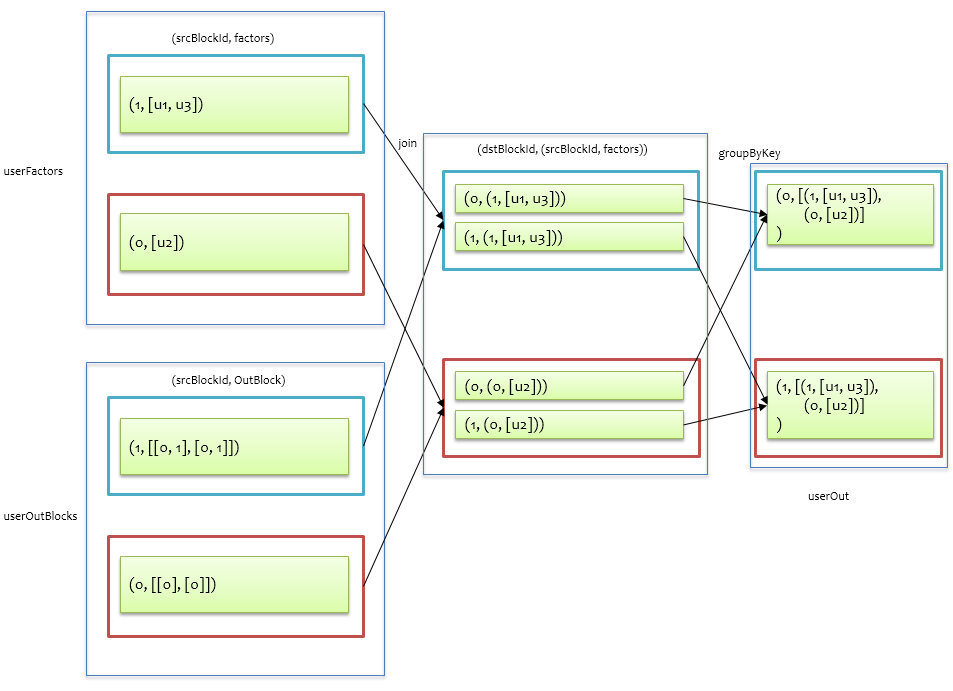
完成了从 u 到 v 的信息发送,后面就是基于 v 的入口信息来收集来自不同 u 的信息了,计算 v 的入口信息跟计算 u 的入口信息一样,只是先要把打分数据blockRatings的src和dst交换一下,如下图所示。
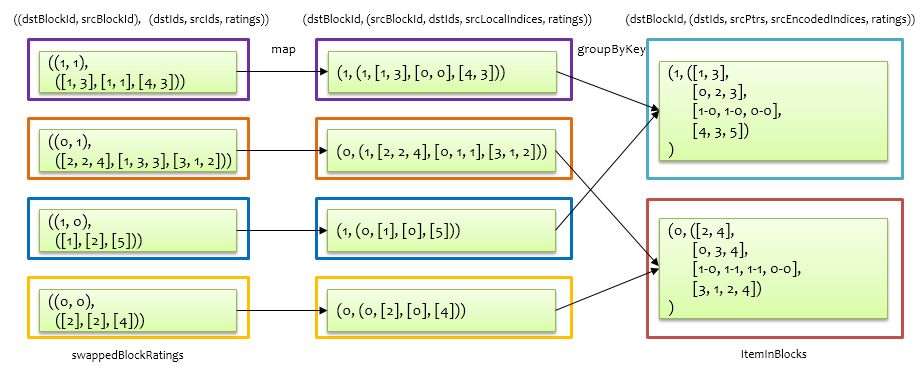
将itemInBlocks与前面的userOut做join,即可将具有相同dstBlockId的记录拉到一起,userOut中包含来自 u 的信息,itemInBlocks包含了与src的对应关系以及打分数据,针对每个 v 找到所有给它发送信息的 u,进而套最小二乘正规方程计算得到itemFactors。
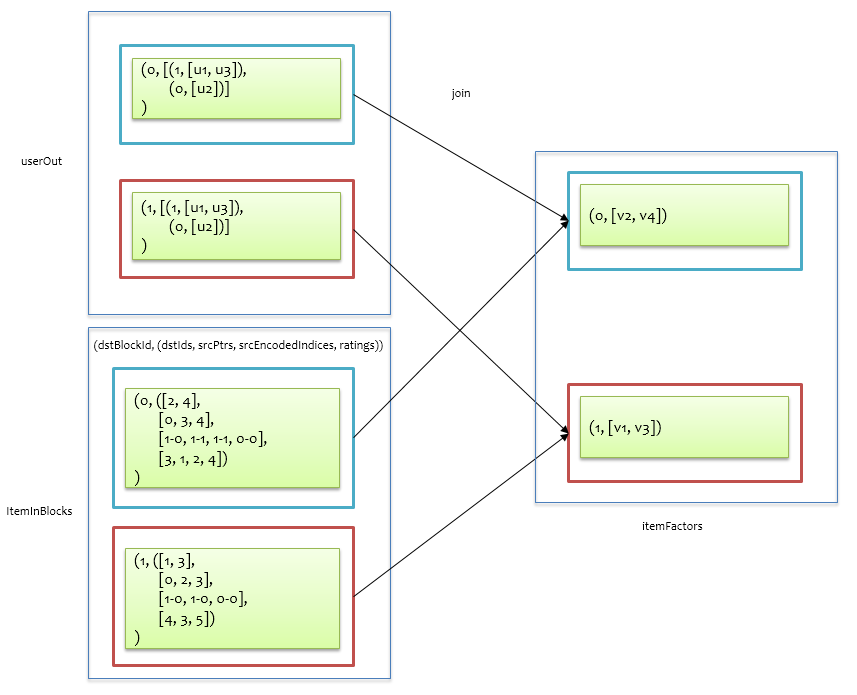
得到itemFactors后可以以同样的方法基于 $V$ 求解 $U$,如此交替求解,直到最大迭代次数为止。
总结
ALS从基本原理上来看应该是很好理解的,但是要通过分布式计算来实现它,相对而言还是较为复杂的,本文重点阐述了Spark ML库中ALS的实现,要看懂以上计算流程,请务必结合源代码理解,凭空理解上述流程可能比较困难,在实际源码实现中,使用了很多优化技巧,例如使用在分区中的索引代替实际uid或vid,实现Int代替Long,使用数组等连续内存数据结构避免由于过多对象造成JVM GC后的内存碎片等。
转载请注明出处,本文永久链接:https://sharkdtu.github.io/posts/ml-als.html

