运用TensorFlow处理简单的NLP问题

当前“人工智能”是继“大数据”后又一个即将被毁的词，每家公司都宣称要发力人工智能，就跟4-5年前大数据一样，业界叫的都非常响亮，不禁想到之前一个老外说过的话：

Big Data is like teenage sex: Everyone talks about it, nobody really knows how to do it, everyone thinks everyone else is doing it, so everyone claims.

现在看来，上面的”Big Data”可以换成”AI”了，在大家还没搞明白大数据的时候，人工智能就开始引领下一个潮流了。本着跟风的态度，我也尝试去窥探个究竟。

引言

当前无论是学术界还是工业界，深度学习都受到极大的追捧，尤其是在Google开源深度学习平台TensorFlow之后，更是给深度学习火上浇油。目前在开源社区Github上所有开源项目中，TensorFlow最为活跃，从推出到现在，经历了几个版本的演进，可以说能够灵活高效地解决大量实际问题。本文主要尝试阐述TensorFlow在自然语言处理(NLP)领域的简单应用，让大家伙儿更加感性地认识TensorFlow。

说到NLP，其实我对它并不是很熟悉，之前也未曾有过NLP的相关经验，本文是我最近学习TensorFlow的一些积累，就当抛砖引玉了。当前互联网每天都在产生大量的文本和音频数据，通过挖掘这些数据，我们可以做一些更加便捷的应用，例如机器翻译、语音识别、词性标注以及信息检索等，这些都属于NLP范畴。而在NLP领域中，语言模型是最基本的一个环节，本文主要围绕语言模型展开，首先介绍其基本原理，进而引出词向量(word2vec)、循环神经网络(RNN)、长短时记忆网络(LSTM)等深度学习相关模型，并详细介绍如何利用 TensorFlow 实现上述模型。

语言模型

语言模型是一种概率模型，它是基于一个语料库创建，得到每个句子出现的概率，通俗一点讲就是看一句话是不是正常人说出来的，数学上表示为:

$$ P(W) = P(w_1 w_2 … w_t) = P(w_1) P(w_2|w_1) P(w_3|w_1 w_2) \cdots P(w_t|w_1 w_2 \cdots w_{t-1}) \tag{2-1}$$

上述公式的意义是：一个句子出现的概率等于给定前面的词情况下，紧接着后面的词出现的概率。它是通过条件概率公式展开得到。其中条件概率 $P({w_2|w_1}), P({w_3|w_1 w_2}), \cdots, P({w_t|w_1 w_2 \cdots w_{t-1}})$ 就是创建语言模型所需要的参数，每个条件概率的意义解释为:根据前面的词预测下一个词的概率。有了这些条件概率参数，给定一个句子，就可以通过以上公式得到一个句子出现的概率。例如有一句话“php是最好的语言”（我不确定这是不是自然语言），假设已经分词为“php”、“是”、“最好的”、“语言”，那么它出现的概率为P(“php”，“是”，“最好的”，“语言”)=P(“php”)P(“是”|“php”)P(“最好的”|“php”，“是”)P(“语言”|“php”，“是”，“最好的”)，如果这个概率较大，那么判断为正常的一句话。以上这些条件概率通过如下贝叶斯公式得到：

$$ P(w_t|w_1 w_2 \cdots w_{t-1}) = \frac {P(w_1 w_2 \cdots w_t)} {P(w_1 w_2 \cdots w_{t-1})} \tag{2-2}$$

根据大数定理上述公式又可以近似为：

$$ P(w_t|w_1 w_2 \cdots w_{t-1}) = \frac {count(w_1 w_2 \cdots w_t)} {count(w_1, w_2, \cdots w_{t-1})} \tag{2-3}$$

假如语料库里有 $N$ 个词，一个句子长度为 $T$ ，那么就有 $N^T$ 种可能，每一种可能都要计算 $T$ 个条件概率参数，最后要计算 $TN^T$ 个参数并保存，不仅计算量大，对于内存要求也是惊人。那么如何避免这个问题呢，之前穷举的方法行不通，那么换个思路，采用一种偷懒的处理方法，就是将上述公式中条件概率做个如下近似：

$$ P(w_t|w_1 w_2 \cdots w_{t-1}) \approx P(w_t|w_{t-n+1} \cdots w_{t-1}) \tag{2-4}$$

这意思就是说一个词出现的概率只与它前面 $n-1$ 个词有关，而不是与它前面所有的词有关，这样极大的减少了统计的可能性，提高了计算效率，这种处理方法称之为 n-gram 模型，通常 $n$ 取2~3就能得到不错的效果。总结起来，n-gram 模型就是统计语料库中词串出现的次数，一次性计算得到词串的概率并将其保存起来，在预测一个句子时，直接通过前面所述的条件概率公式得到句子出现的概率。

近年也流行起神经网络语言模型，从机器学习的角度来看，一开始不全部计算这些词串的概率值，而是通过一个模型对词串的概率进行建模，然后构造一个目标函数，不断优化这个目标，得到一组优化的参数，当需要哪个词串概率时，利用这组优化的参数直接计算得到对应的词串概率。将词串概率 $P(w|{context(w)})$ 看做是 $w$ 和 $context(w)$ 的函数，其中 $context(w)$ 表示此 $w$ 的上下文，即相当于前面所述的 n-gram 模型的前 $n-1$ 个词，那么就有如下数学表示。

$$ P(w|{context(w)}) = F(w, {context(w)}, \Theta) \tag{2-5}$$

目标函数采用对数似然函数，表示如下(其中 $N$ 代表语料库中词典的大小)：

$$ Obj = \frac{1}{N} \sum \limits_{i = 1}^N log P({w_i}|{context_i}) \tag{2-6}$$

通过优化算法不断最小化目标函数得到一组优化的参数 $\Theta$ ，在神经网络中参数 $\Theta$ 则为网络层与层间的权值与偏置。那么在用神经网络学习语言模型[1]时，如何表示一个词呢？通常，在机器学习领域，是将一个样本对象抽象为一个向量，所以类似地，神经网络语言模型中是将词(或短语)表示为向量，通常叫做word2vec。那么神经网络语言模型就可以表示如下示意图。

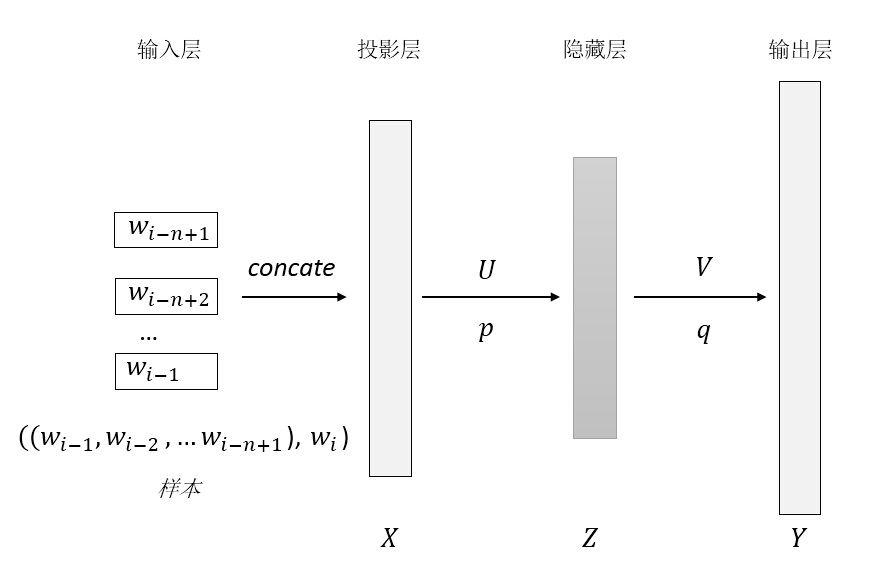
上述神经网络包括输入层、投影层、隐藏层以及输出层，其中投影层只是对输入层做了一个预处理，将输入的所有词进行一个连接操作，假如一个词表示为 $m$ 维向量，那么由 $n-1$ 个词连接后则为 $(n-1)m$ 维向量，将连接后的向量作为神经网络的输入，经过隐藏层再到输出层，其中 $W$ 、$U$ 分别为投影层到隐藏层、隐藏层到输出层的权值参数，$p$ 、$q$ 分别为投影层到隐藏层、隐藏层到输出层的偏置参数，整个过程数学表达如下：

$$
\begin{split}
Z &= \sigma(WX + p)\\
Y &= UZ + q
\end{split} \tag{2-7}
$$

其中 $\sigma$ 为sigmoid函数，作为隐藏层的激活函数，输出层的输出向量为 $N$ 维，对应于语料库中词典的大小。一般需要再经过softmax归一化为概率形式，得到预测语料库中每个词的概率。以上神经网络语言模型看似很简单，但是词向量怎么来呢，如何将一个词转化为向量的形式呢？下面作详细阐述。

词向量(word2vec)

词向量要做的事就是将语言数学化表示，以往的做法是采用 One-hot Representation 表示一个词，即语料库词典中有 $N$ 个词，那么向量的维度则为 $N$ ，给每个词编号，对于第 $i$ 个词，其向量表示除了第 $i$ 个单元为1，其他单元都为0的 $N$ 维向量，这种词向量的缺点显而易见，一般来说语料库的词典规模都特别大，那么词向量的维数就非常大，并且词与词之间没有关联性，并不能真实地刻画语言本身的性质，例如“腾讯”、“小马哥”这两个词通过One-hot向量表示，没有任何关联。为了克服One-hot Representation 的缺点，Mikolov大神提出了一种 Distributed Representation[2]，说个题外话，在大家都在如火如荼的用CNN做图像识别的时候，这哥们却在研究如何用神经网络处理NLP问题，最后发了大量关于神经网络NLP的高水平论文，成为这一领域的灵魂人物之一。顾名思义，Distributed Representation 就是把词的信息分布到向量不同的分量上，而不是像 One-hot Representation 那样所有信息集中在一个分量上，它的做法是将词映射到 $m$ 维空间，表示为 $m$ 维向量，也称之为 Word Embedding，这样一方面可以减小词向量的维度，另一方面，可以将有关联的词映射为空间中相邻的点，词与词之间的关联性通过空间距离来刻画，如下图所示。

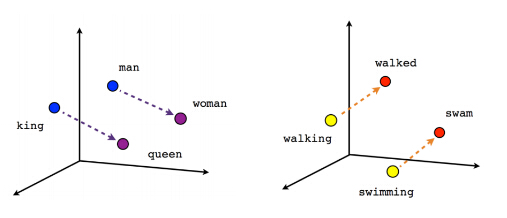
词被映射到3维空间，每个词表示为一个3维向量，相近的词离的较近，可以看到两组差不多关系的词，他们之间的词向量距离也差不多。

要想得到词向量，需要借助语言模型训练得到，本质上来说，词向量是在训练语言模型过程中得到的副产品。解决word2vec问题有两种模型，即 CBOW 和 Skip-Gram 模型[3]，如下图所示：

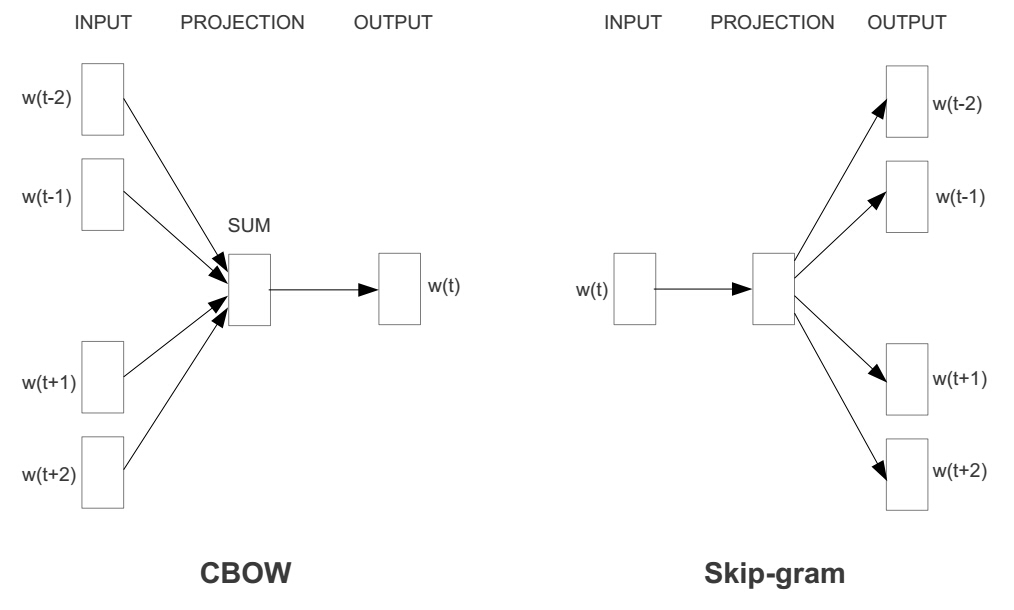
CBOW 模型是根据词的上下文预测当前词，这里的上下文是由待预测词的前后 $c$ 个词组成。而 Skip-Gram 模型则相反，是通过当前词去预测上下文。给定一个语料库作为训练集，就可以通过以上模型训练出每个词的向量表示。从实验结果来看，CBOW 模型会平滑掉一些分布信息，因为它将词的上下文作为单个样本，而 Skip-Gram 模型将词上下文拆分为多个样本，训练得到的结果更为精确，为此，TensorFlow 中 word2vec 采用的是 Skip-Gram 模型，对应于文[2]中所提出的一种更为优化的 Skip-Gram 模型，下面着重介绍其原理，更多关于 CBOW 和 Skip-Gram 模型细节可以参阅文[3]。

Skip-Gram 模型

前面也提到， Skip-Gram 模型是根据当前词去预测上下文，例如有如下语句：

“php 是世界上最好的语言”

假定上下文是由待预测词的前后2个词组成，那么由以上句子可以得到如下正样本：

(世界上, 是), (世界上, php), (世界上, 最好的), (世界上, 语言), (最好的, 世界上), …

训练目标为最大化以下对数似然函数：

$$ Obj = \frac {1} {N} \sum_{i=1}^{N} \sum_{-c \leqslant j \leqslant c , j \neq 0} log \ p(w_{i+j}|w_i) \tag{3-1}$$

其中 $c$ 为上下文的距离限定，即仅取词 $w_t$ 的前后 $c$ 个词进行预测。$c$ 越大，训练结果更精确，但是计算复杂度加大，训练成本相应也更大，一般取 $c$ 为2～3就能训练出不错的结果。基本的 Skip-Gram 模型采用softmax方法将以上目标函数中概率 $p(w_{i+j}|w_i)$ 定义为：

$$ p(w_O|w_I) = \frac {exp({\theta_{w_O}}^T v_{w_I})} {\sum_{w\in W} exp({\theta_{w}}^T v_{w_I})} \tag{3-2}$$

其中 $v_w$ 表示输入词 $w$ 的向量，$\theta_{w}$ 表示预测结果为 $w$ 的权值参数，二者都是待训练的参数。不难发现，通过以上公式，计算每个词的损失函数都要用到词典中的所有词，而一般词典的量级都非常大，所以这种方式是不切实际的。对于一个样本，例如(“世界上”, “php”)，无非是根据词“世界上”去预测词“php”，那么就可以看成一个二分类问题，对于输入词“世界上”，预测“php”为正，预测其他则为负，其他词可能是除“php”以外的所有词，为了简化计算，可以通过采样的方式，每次随机从所有除“php”以外的词中取 $k$ 个词作为负样本对象，那么训练目标则可以转化为类似于逻辑回归目标函数：

$$ Obj = log \sigma ({\theta_{w_O}}^{T} v_{w_I}) + \sum_{j=1}^{k} E_{w_j\sim {P_n}(w)} [log \sigma (-{\theta_{w_j}}^{T} v_{w_I})] \tag{3-3}$$

以上表达式称之为 NCE(Noise-contrastive estimation)[4]目标函数，其中等号右边第二项表示通过一个服从 $P_{n}(w)$ 分布的采样算法取得 $k$ 个负样本的期望损失。文[2]中采用了一个简单的一元分布采样，简化了计算，称之为负采样(Negative Sampling)，下面详细介绍负采样算法。

负采样算法

词典中的每个词在语料库中出现的频次有高有低，理论上来说，对于那些高频词，被选为负样本的概率较大，对于那些低频词，被选为负样本的概率较小。基于这个基本事实，可以通过带权采样方法来实现，假设每个词的词频表示为单位线段上的一小分段，对于词典大小为 $N$ 的语料库，可以将词典中所有的词表示为单位线段上的一点，再在单位线段上等距离划分 $M$ 个等分， $M>>N$ ，具体采样过程就是随机得到一个数 $i<M$，通过映射找到其对应的词，如下如所示。

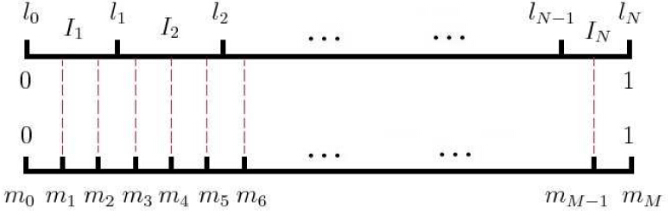
文[2]中在实际负采样计算词频时，做了一点修正，不是简单的统计词的出现次数，而是对词的出现次数做了 $\alpha$ 次幂处理，最后词频公式为：

$$ freq(w) = \frac {[counter(w)]^{3/4}} {\sum_{u \in W} [counter(u)]^{3/4}} \tag{3-4}$$

高频词二次采样

在一个大语料库中，很多常见的词大量出现，如“的”、“是”等。这些词虽然词频较高，但是能提供的有用信息却很少。一般来说，这些高频词的词向量在训练几百万样本后基本不会有太大的变化，为了提高训练速度，平衡低频词和高频词，文[2]中提出一种针对高频词二次采样的技巧，对于每个词，按如下概率丢弃而不做训练。

$$ P(w_i) = 1 - \sqrt{\frac{t}{f(w_i)}} \tag{3-5}$$

其中$f(w_i)$表示词频，从上述公式中不难发现，二次采样仅针对那些满足 $f(w_i) > t$ 所谓的高频词有效，参数 $t$ 根据语料库的大小而设置，一般设置为 $10^{-5}$ 左右。

TensorFlow实现

根据以上实现原理，下面结合代码阐述利用TensorFlow实现一个简易的word2vec模型[5]，借助TensorFlow丰富的api以及强大的计算引擎，我们可以非常方便地表达模型。给定语料库作为训练数据，首先扫描语料库建立字典，为每个词编号，同时将那些词频低于min_count的词过滤掉，即不对那些陌生词生成词向量。对于一个样本(“世界上”, “php”)，利用负采样得到若干负实例，分别计算输入词为“世界上”到“php”以及若干负样本的logit值，最后通过交叉熵公式得到目标函数(3-3)。

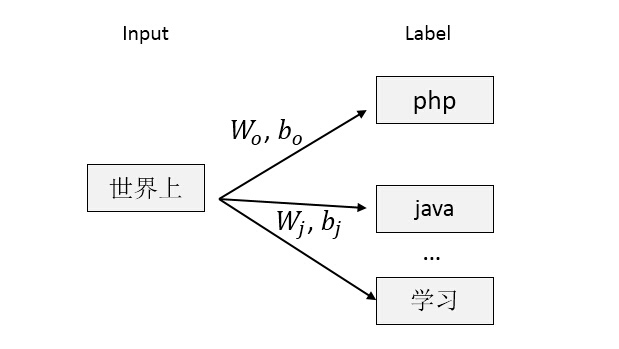
构建计算流图

首先定义词向量矩阵，也称为 embedding matrix，这个是我们需要通过训练得到的词向量，其中vocabulary_size表示词典大小，embedding_size表示词向量的维度，那么词向量矩阵为 vocabulary_size $\times$ embedding_size，利用均匀分布对它进行随机初始化：

1 2	embeddings = tf.Variable( tf.random_uniform([vocabulary_size, embedding_size], -1.0, 1.0))

定义权值矩阵和偏置向量（对应于3-3式中的 $\theta$），并初始化为0：

weights = tf.Variable(
  tf.truncated_normal([vocabulary_size, embedding_size],
                      stddev=1.0 / math.sqrt(embedding_size)))
biases = tf.Variable(tf.zeros([vocabulary_size]))

给定一个batch的输入，从词向量矩阵中找到对应的向量表示，以及从权值矩阵和偏置向量中找到对应正确输出的参数，其中examples是输入词，labels为对应的正确输出，一维向量表示，每个元素为词在字典中编号：

# Embeddings for examples: [batch_size, embedding_size]
example_emb = tf.nn.embedding_lookup(embeddings, examples)
# Weights for labels: [batch_size, embedding_size]
true_w = tf.nn.embedding_lookup(weights, labels)
# Biases for labels: [batch_size, 1]
true_b = tf.nn.embedding_lookup(biases, labels)

负采样得到若干非正确的输出，其中labels_matrix为正确的输出词，采样的时候会跳过这些词，num_sampled为采样个数，distortion即为公式(3-4)中的幂指数：

labels_matrix = tf.reshape(
    tf.cast(labels,
            dtype=tf.int64),
    [batch_size, 1])
# Negative sampling.
sampled_ids, _, _ = tf.nn.fixed_unigram_candidate_sampler(
     true_classes=labels_matrix,
     num_true=1,
     num_sampled=num_samples,
     unique=True,
     range_max=vocab_size,
     distortion=0.75,
     unigrams=vocab_counts.tolist())

找到采样样本对应的权值和偏置参数：

# Weights for sampled ids: [num_sampled, embedding_size]
sampled_w = tf.nn.embedding_lookup(weights, sampled_ids)
# Biases for sampled ids: [num_sampled, 1]
sampled_b = tf.nn.embedding_lookup(biases, sampled_ids)

分别计算正确输出和非正确输出的logit值，即计算 $WX + b$，并通过交叉熵得到目标函数(3-3)：

# True logits: [batch_size, 1]
true_logits = tf.reduce_sum(tf.mul(example_emb, true_w), 1) + true_b
# Sampled logits: [batch_size, num_sampled]
# We replicate sampled noise lables for all examples in the batch
# using the matmul.
sampled_b_vec = tf.reshape(sampled_b, [num_samples])
sampled_logits = tf.matmul(example_emb,
                           sampled_w,
                           transpose_b=True) + sampled_b_vec
# cross-entropy(logits, labels)
true_xent = tf.nn.sigmoid_cross_entropy_with_logits(
   true_logits, tf.ones_like(true_logits))
sampled_xent = tf.nn.sigmoid_cross_entropy_with_logits(
   sampled_logits, tf.zeros_like(sampled_logits))
# NCE-loss is the sum of the true and noise (sampled words)
# contributions, averaged over the batch.
loss = (tf.reduce_sum(true_xent) +
        tf.reduce_sum(sampled_xent)) / batch_size

训练模型

计算流图构建完毕后，我们需要去优化目标函数。采用梯度下降逐步更新参数，首先需要确定学习步长，随着迭代进行，逐步减少学习步长，其中trained_words为已训练的词数量，words_to_train为所有待训练的词数量：

1 2	lr = init_learning_rate * tf.maximum( 0.0001, 1.0 - tf.cast(trained_words, tf.float32) / words_to_train)

定义优化算子，使用梯度下降训练模型：

optimizer = tf.train.GradientDescentOptimizer(lr)
train = optimizer.minimize(loss,
                           global_step=global_step,
                           gate_gradients=optimizer.GATE_NONE)
session.run(train)

验证词向量

经过以上步骤后，即可得到词向量矩阵，即上述代码中的变量embeddings，那么如何验证得到的词向量矩阵的好坏呢，Mikolov等人发现[2]，如果一对关系差不多的词，其词向量在空间中的连线近乎平行，如下图所示。

为此，给定基准测试集，其每行包含4个词组成一个四元组 $(w_1, w_2, w_3, w_4)$ ，对于一个较好的词向量结果，每个四元组大致会有如下关系：

$$ Vector(w_1) - Vector(w_2) + Vector(w_4) = Vector(w_3) $$

循环神经网络(RNN)

人类不是从脑子一片空白开始思考，当你读一篇文章的时候，你会根据前文去理解下文，而不是每次看到一个词后就忘掉它，理解下一个词的时候又从头开始。传统的神经网络模型是从输入层到隐藏层再到输出层，每层之间的节点是无连接的，这种普通的神经网络不具备记忆功能，而循环神经网络(Recurrent Neural Network，RNN)就是来解决这类问题，它具备记忆性，通常用于处理时间序列问题，在众多NLP问题中，RNN取得了巨大成功以及广泛应用。

在RNN网络中，一个序列当前的输出除了与当前输入有关以外，还与前面的输出也有关，下图为RNN中一个单元的结构示意图，图片来源于文[7]。

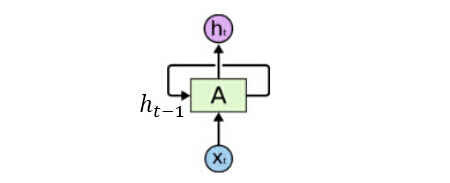
上图理解起来可能还不是很形象，根据时间序列将上图平铺展开得到如下图，其链式的特征揭示了 RNN 本质上是与序列相关的，所以 RNN 对于这类数据来说是最自然的神经网络架构。

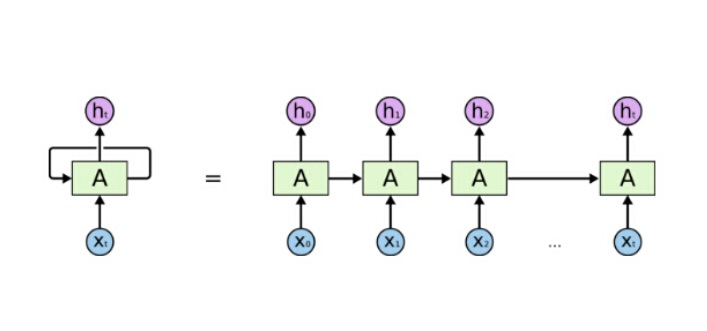
然而 RNN 有一个缺点，虽然它可以将之前的信息连接到当前的输入上，但是如果当前输入与之前的信息时间跨度很大，由于梯度衰减等原因，RNN 学习如此远的信息的能力会下降，这个问题称之为长时间依赖（Long-Term Dependencies）问题。例如预测一句话“飞机在天上”下一个词，可能不需要太多的上下文就可以预测到下一个词为“飞”，这种情况下，相关信息与要预测的词之间的时间跨度很小，RNN 可以很容易学到之前的信息。再比如预测“他来自法国，…，他会讲”的下一个词，从当前的信息来看，下一个词可能是一种语言，但是要想准确预测哪种语言，就需要再去前文找信息了，由于前文的“法国”离当前位置的时间跨度较大，RNN很难学到如此远的信息。更多长时间依赖细节参考文[8]。幸运的是，有一种 RNN 变种，叫做长短时记忆网络(Long Short Term Memory networks, LSTM)，可以解决这个问题。

长短时记忆网络(LSTM)

LSTM 是一种带有选择性记忆功能的 RNN，它可以有效的解决长时间依赖问题，并能学习到之前的关键信息。如下图所示为 LSTM 展开后的示意图。

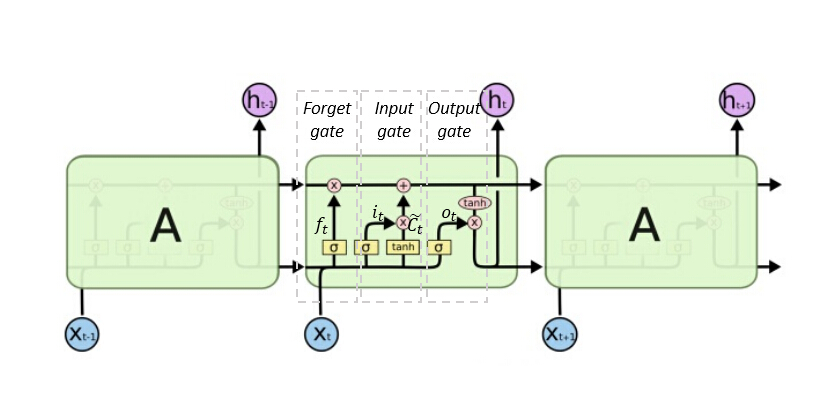
相对于 RNN , LSTM 只是在每个单元结构上做了改进，在 RNN 中，每个单元结构只有单个激活函数，而 LSTM 中每个单元结构更为复杂，它增加了一条状态线（图中最上面的水平线），以记住从之前的输入学到的信息，另外增加三个门(gate)来控制其该状态，分别为忘记门、输入门和输出门。忘记门的作用是选择性地将之前不重要的信息丢掉，以便存储新信息；输入门是根据当前输入学习到新信息然后更新当前状态；输出门则是结合当前输入和当前状态得到一个输出，该输出除了作为基本的输出外，还会作为下一个时刻的输入。下面用数学的方式表达每个门的意思。

忘记门，要丢掉的信息如下：

$$ f_t = \sigma (W_f[h_{t-1}, x_t] + b_f) \tag{5-1}$$

输入门，要增加的信息如下：
$$
\begin{split}
i_t &= \sigma (W_i[h_{t-1}, x_t] + b_i)\\
\tilde{C_t} &= tanh(W_C[h_{t-1}, x_t] + b_C)
\end{split} \tag{5-2}
$$

那么根据忘记门和输入门，状态更新如下：

$$ C_t = f_t * C_{t-1} + i_t * \tilde{C_t} \tag{5-3}$$

输出门，得到输出信息如下：

$$
\begin{split}
o_t &= \sigma (W_o[h_{t-1}, x_t] + b_o)\\
h_t &= o_t * tanh(C_t)
\end{split} \tag{5-4}
$$

LSTM 单元输入都是上一个时刻的输出与当前时刻的输入通过向量concat连接而得到，基于这个输入，利用sigmoid函数作为三个门的筛选器，分别得到 $f_t$ 、$i_t$ 、$o_t$，这三个筛选器分别选择部分分量对状态进行选择性忘记、对输入进行选择性输入、对输出进行选择性输出。以上是 LSTM 基本结构原理，在这基础上，根据不同的实际应用场景，演变出很多 LSTM 的变体，更多关于 LSTM 的详细解释请参考文[7]。下面介绍一种深层 LSTM 网络[9]，该结构也是 TensorFlow 中 LSTM 所实现的根据[10]。

深层LSTM网络

深度学习，其特点在于深，前面已经讲述单层 LSTM 网络结构，深层 LSTM 网络其实就是将多层 LSTM 叠加，形成多个隐藏层，如下图所示。

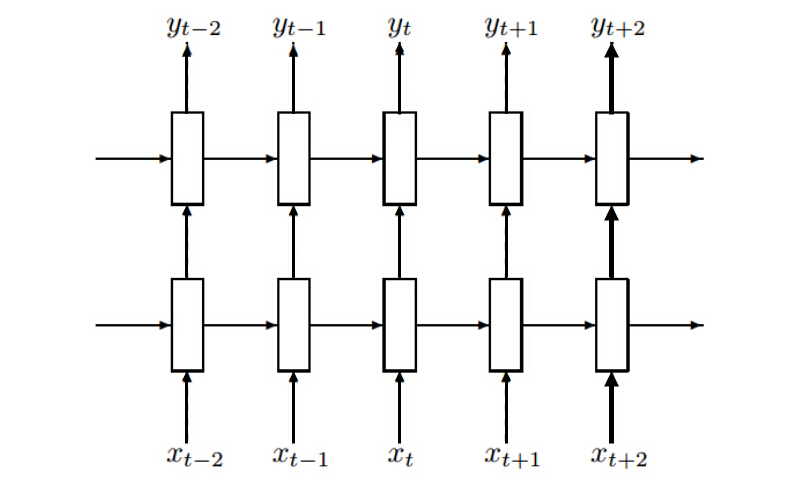
上图中每个 LSTM 单元内部结构如下图所示，对于 $l$ 层 $t$ 时刻来说，$h_{t-1}^l$ 为 $l$ 层 $t-1$ 时刻（即上一个时刻）的输出，$h_t^{l-1}$ 为 $l-1$ 层（即上一层） $t$ 时刻的输出，这两个输出叠加作为 $l$ 层 $t$ 时刻的输入。

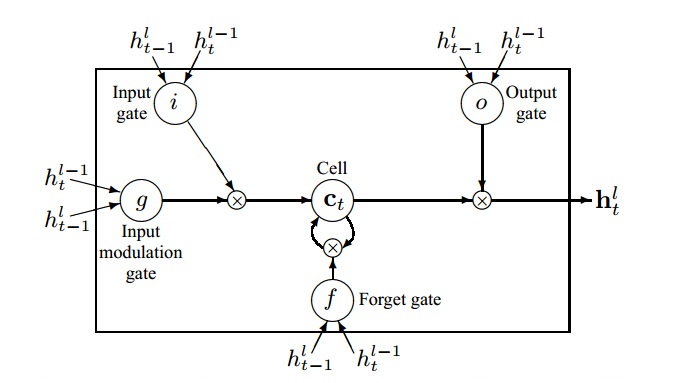
根据上面的结构，可以得到 $l$ 层 LSTM 数学表达, $h_t^{l-1}, h_{t-1}^l, c_{t-1}^l \rightarrow h_t^l, c_t^l$：

$$
\begin{split}
f &= \sigma (W_f[h_t^{l-1}, h_{t-1}^l] + b_f) \\
i &= \sigma (W_i[h_t^{l-1}, h_{t-1}^l] + b_i) \\
o &= \sigma (W_o[h_t^{l-1}, h_{t-1}^l] + b_o) \\
g &= tanh(W_g[h_t^{l-1}, h_{t-1}^l] + b_g) \\
\ \notag \\
c_t^l &= f * c_{t-1}^l + i * g \\
h_t^l &= o * tanh(c_t^l)
\end{split} \tag{5-5}
$$

其中 $c_{t-1}^l$ 表示上一时刻的状态，$c_t^l$ 表示由当前输入更新后的状态。

正则化

然而，实践证明大规模的 LSTM 网络很容易过拟合，实际应用中，需要采取正则化方法来避免过拟合，神经网络中常见的正则化方法是Dropout方法[11]，文[12]提出一种简单高效的Dropout方法运用于 RNN/LTSM 网络。如下图所示，Dropout仅应用于虚线方向的输入，即仅针对于上一层的输出做Dropout。

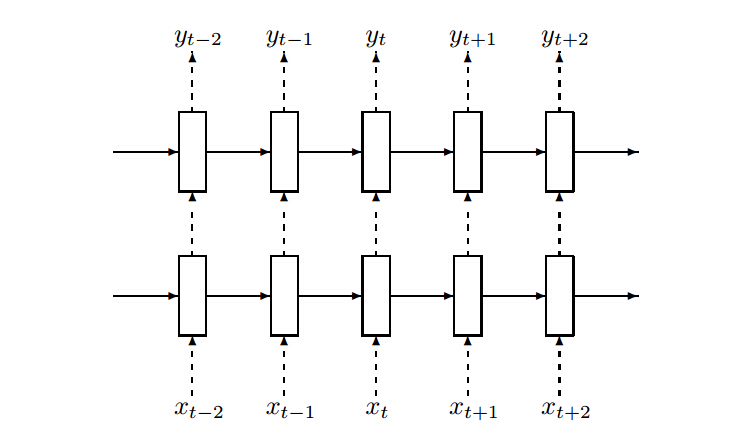
根据上图的Dropout策略，公式(5-5)可以改写成如下形式：

$$
\begin{split}
f &= \sigma (W_f[D(h_t^{l-1}), h_{t-1}^l] + b_f) \\
i &= \sigma (W_i[D(h_t^{l-1}), h_{t-1}^l] + b_i) \\
o &= \sigma (W_o[D(h_t^{l-1}), h_{t-1}^l] + b_o) \\
g &= tanh(W_g[D(h_t^{l-1}), h_{t-1}^l] + b_g) \\
\ \notag \\
c_t^l &= f * c_{t-1}^l + i * g \\
h_t^l &= o * tanh(c_t^l)
\end{split} \tag{5-6}
$$

其中 $D$ 表示Dropout操作符，会随机地将 $h_t^{l-1}$ 的中的分量设置为零。如下图所示，黑色粗实线表示从 $t-2$ 时刻的信息流向 $t+2$ 时刻作为其预测的参考，它经历了 $L+1$ 次的Dropout，其中 $L$ 表示网络的层数。

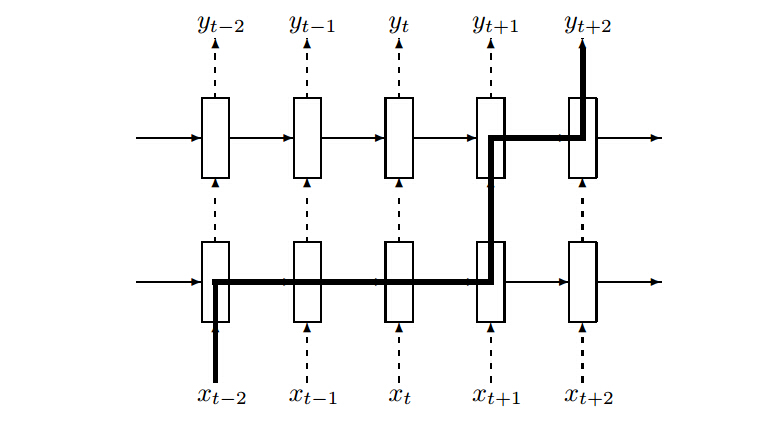
TensorFlow实现

根据前面所述的 LSTM 模型原理，实现之前提到的语言模型，即根据前文预测下一个词，例如输入“飞机在天上”预测下一个词“飞”，使用 TensorFlow 来实现 LSTM 非常的方便，因为 TensorFlow 已经提供了基本的 LSTM 单元结构的Operation，其实现原理就是基于文[12]提出的带Dropout的 LSTM 模型。完整代码请参考ptb_word_lm.py

构建LSTM模型

利用TensorFlow提供的Operation，实现 LSTM 网络很简单，首先定义一个基本的 LSTM 单元，其中size为 LSTM 单元的输出维度，再对其添加Dropout，根据 LSTM 的层数num_layers得到多层的 RNN 结构单元。

lstm_cell = tf.nn.rnn_cell.BasicLSTMCell(size, forget_bias=0.0)
lstm_cell = tf.nn.rnn_cell.DropoutWrapper(
    lstm_cell, output_keep_prob=keep_prob)
cell = tf.nn.rnn_cell.MultiRNNCell([lstm_cell] * num_layers)

每次给定一个batch的输入，将 LSTM 网络的状态初始化为0。词的输入由词向量表示，所以先定义一个embedding矩阵，这里可以不要关心它一开始有没有，它会在训练过程中的慢慢得到的，仅作为训练的副产品。假设LSTM网络展开num_steps步，每一步给定一个batch的词作为输入，经过 LSTM 单元处理后，状态更新并得到输出，并通过softmax归一化后计算损失函数。

initial_state = cell.zero_state(batch_size, tf.float32)
embedding = tf.get_variable("embedding", [vocab_size, size])
# input_data: [batch_size, num_steps]
# targets： [batch_size, num_steps]
input_data = tf.placeholder(tf.int32, [batch_size, num_steps])
targets = tf.placeholder(tf.int32, [batch_size, num_steps])
inputs = tf.nn.embedding_lookup(embedding, input_data)
outputs = []
for time_step in range(num_steps):
  (cell_output, state) = cell(inputs[:, time_step, :], state)
  outputs.append(cell_output)

output = tf.reshape(tf.concat(1, outputs), [-1, size])
softmax_w = tf.get_variable("softmax_w", [size, vocab_size])
softmax_b = tf.get_variable("softmax_b", [vocab_size])
logits = tf.matmul(output, softmax_w) + softmax_b

loss = tf.nn.seq2seq.sequence_loss_by_example(
    [logits],
    [tf.reshape(targets, [-1])],
    [tf.ones([batch_size * num_steps])])

训练模型

简单采用梯度下降优化上述损失函数，逐步迭代，直至最大迭代次数，得到final_state，即为LSTM所要学习的参数。

optimizer = tf.train.GradientDescentOptimizer(lr)
train_op = optimizer.minimize(loss)
for i in range(max_epoch):
  _, final_state = session.run([train_op, state],
                               {input_data: x,
                                targets: y})

验证测试模型

模型训练完毕后，我们已经得到LSTM网络的状态，给定输入，经过LSTM网络后即可得到输出了。

1 2	(cell_output, _) = cell(inputs, state) session.run(cell_output)

小结

在使用TensorFlow处理深度学习相关问题时，我们不需要太关注其内部实现细节，只需把精力放到模型的构建上，利用TensorFlow已经提供的抽象单元结构就可以构建灵活的模型。也恰恰正是因为TensorFlow的高度抽象化，有时让人理解起来颇费劲。所以在我们使用TensorFlow的过程中，不要把问题细化的太深，一切数据看成Tensor即可，利用Tensor的操作符对其进行运算，不要在脑海里想如何如何的运算细节等等，不然就会身陷囹圄。

参考文献

[1]. Bengio Y, Schwenk H, Senécal J S, et al. Neural probabilistic language models[M]//Innovations in Machine Learning. Springer Berlin Heidelberg, 2006: 137-186.MLA.
[2]. Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]//Advances in neural information processing systems. 2013: 3111-3119.
[3]. Mikolov T, Le Q V, Sutskever I. Exploiting similarities among languages for machine translation[J]. arXiv preprint arXiv:1309.4168, 2013.
[4]. Gutmann M U, Hyvärinen A. Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics[J]. The Journal of Machine Learning Research, 2012, 13(1): 307-361.
[5]. Vector Representations of Words. https://www.tensorflow.org/versions/r0.8/tutorials/word2vec/index.html#vector-representations-of-words
[6]. word2vec 中的数学原理详解. http://www.cnblogs.com/peghoty/p/3857839.html
[7]. Understanding LSTM Networks. http://colah.github.io/posts/2015-08-Understanding-LSTMs/
[8]. Bengio Y, Simard P, Frasconi P. Learning long-term dependencies with gradient descent is difficult[J]. Neural Networks, IEEE Transactions on, 1994, 5(2): 157-166.
[9]. Graves A. Generating sequences with recurrent neural networks[J]. arXiv preprint arXiv:1308.0850, 2013.
[10]. Recurrent Neural Networks. https://www.tensorflow.org/versions/r0.8/tutorials/recurrent/index.html#recurrent-neural-networks
[11]. Srivastava N. Improving neural networks with dropout[D]. University of Toronto, 2013.
[12]. Zaremba W, Sutskever I, Vinyals O. Recurrent neural network regularization[J]. arXiv preprint arXiv:1409.2329, 2014.

转载请注明出处，本文永久链接：https://sharkdtu.github.io/posts/nn-nlp.html