模型简介
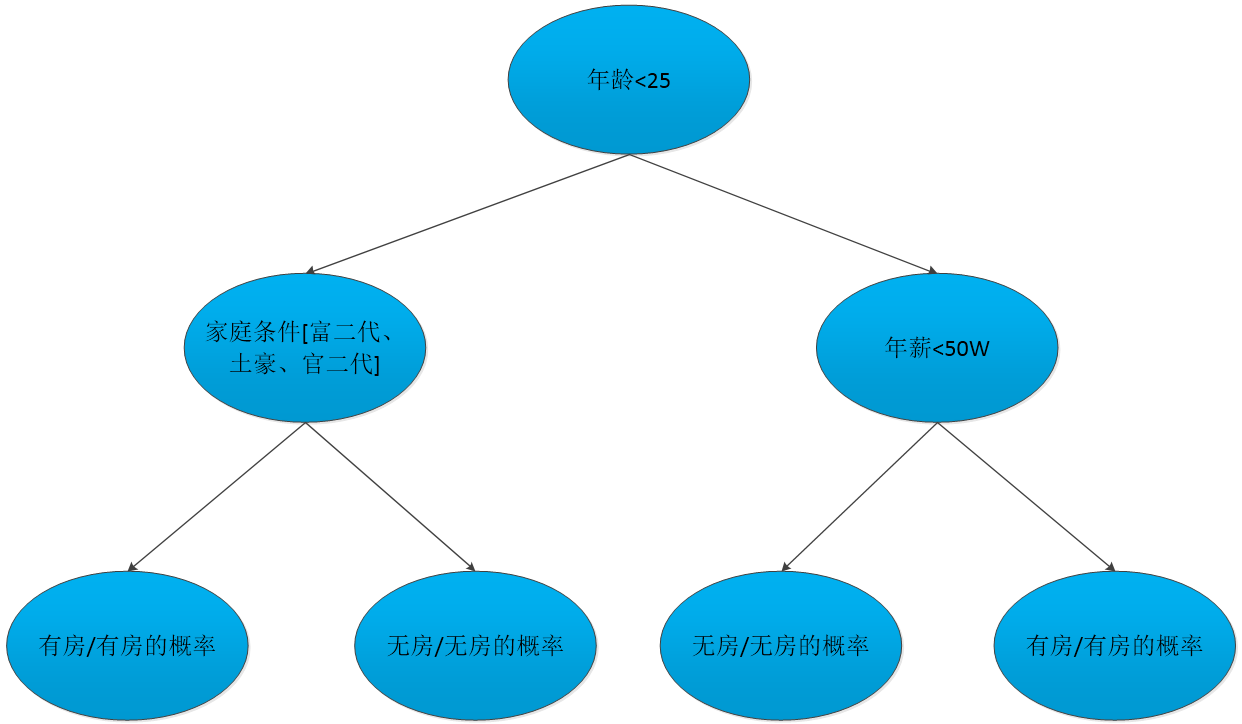
决策树是一种常见的分类与回归机器学习算法,由于其模型表达性好,便于理解,并能取得较好的效果,而受到广泛的应用。下图是一个简单的决策树,决策树每个非叶子节点包含一个条件,对于具有连续值的特征,该条件为一个上界,如果实例对应的特征值小于该上界则被划分到左子节点,否则被划分到右子节点,对于具有离散值的特征,该条件为一个子集,如果实例对应的特征值属于该子集则被划分到左子节点,否则被划分到右子节点。如此下去,一个实例从根节点开始,不断地被划分,直到叶子节点。对于分类问题,叶子节点输出其类别,对于回归问题,叶子节点输出其分值或概率。
给定训练数据,如何学习决策树模型呢?首先将决策树抽象为一般的机器学习问题,用数学的说法就是,一个决策树对应着输入空间的一个划分以及在划分单元上的输出值。假设已经将输入空间划分为 $m$ 个单元(即叶子节点) $R_1, R_2,… R_m$,在每个单元 $R_i$ 上有一个固定的输出 $c_i$,那么决策树模型可表示为:
$$ f(x) = \sum_{i}^m c_i I(x \in R_i) $$
一般的机器学习算法是找一个目标函数,然后不断地去优化目标,直至训练误差在允许的范围内,得到模型参数。决策树的学习则采用启发式的方法,从根节点开始,根据该节点上的训练样本找到最优切分点,将训练样本划分为两个子集,一般来说,对于分类问题,每个子集采用多数表决的方式决定类别,对于回归问题,每个子集输出其中所有样本的平均值;每一次划分的依据是,划分后相对于划分前,不确实性有所减少,上述最优切分点就是不确定性减少的最多的切分方案,这里的不确定性可以是熵、基尼系数、平方误差、方差等;为了防止过拟合,需要设定划分的终止条件,通常有如下限制:1)树的最大深度,2)一次划分至少减少的不确定,3)一次划分后,子集中至少包含的样本实例数。
决策树的训练
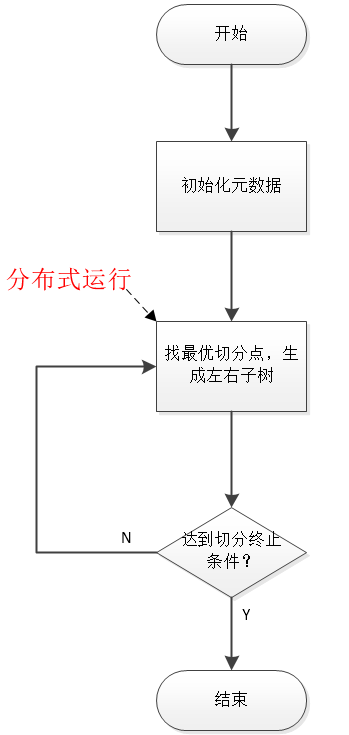
MLlib中决策树的学习同样是利用前面所述的启发式方法,借助RDD进行分布式计算,其本质上是数据并行。下面是mllib中决策树学习的总体流程图,其最关键的一步就是如何找最优切分点,首先简单介绍下前后两步:初始化元数据以及如何判断切分终止条件,由于这两步实质上是由用户的参数配置和训练样本决定,暂且统称为算法参数,然后再着重详细讨论mllib如何分布式计算最优切分点。
算法参数
算法参数是由训练数据以及用户的参数配置共同决定,mllib提供给用户的自定义参数是通过类Strategy来封装,下面列出一些重要的参数并详细说明其意义:
- algo:指定决策树的类型,有分类树(classification)和回归树(Regression)
- numClasses:如果是分类树,指定有多少种类别
- subsamplingRate:训练样本采样率,如果在(0,1)之间则表明采样部分训练数据进行训练
- impurity:指定不确定性指标,其中基尼系数(Gini)、熵(Entropy)用于分类树,方差(Variance)用于回归树
- minInfoGain:每次切分至少减少的不确定性,否则停止切分,用于终止迭代计算
- minInstancesPerNode:切分后,每个子节点至少包含的样本实例数,否则停止切分,用于终止迭代计算
- maxDepth:树的最大深度,用于终止迭代计算
- categoricalFeaturesInfo:指定离散特征,是一个map,featureId->K,其中K表示特征值可能的情况(0, 1, …, K-1)
- maxBins:最大分箱数,当某个特征的特征值为连续时,该参数意思是将连续的特征值离散化为多少份
特征划分
训练样本的每个特征可能具有各自的特点,mllib中将特征作如下划分:
- 特征值只在有限的离散值范围内,把这类特征称为 categorical feature,这类特征需要通过配置参数指定,即前面所述的
categoricalFeaturesInfo; - 特征值为连续值,把这类特征称为 continuous feature,这类特征需要对其特征值进行离散化,便于后续的寻找最优切分点。
在初始化元数据阶段,会根据输入的训练数据,得到样本的维度 numFeatures,在每个维度(特征)上计算所有可能的切分方案,在寻找最优切分点阶段会遍历所有可能的切分方案,找出最优的切分点。不同的特征、不同的决策树(分类还是回归),切分方案都不一样,下面作详细介绍。
categorical feature 切分
如果特征是 categorical feature(由参数categoricalFeaturesInfo指定),那么有两种切分方法,对于取值较少的特征,采用不排序切分方法,例如,一个人的收入情况可能有三种情况“高、中、低”,其所有可能的切分方案为“高 | 中低”、“中 | 高低”、“高中 | 低”三种,更一般地,如果一个特征可能的取值为 $k$,那么所有可能的切分方案为 $2^{k-1}-1$ ,被切分后的部分看成一个个箱子(bin),如果被切分为“高 | 中低”,那么其分箱情况为:“高”在一个分箱,“中低”在另一个分箱,不难发现,所有可能的分箱数(bins)为 $2\times(2^{k-1}-1)=2^k-2$,我们把这种特征称为unordered feature,这种切分方法只被用于多分类问题。对于取值较多的特征,如果采用不排序的切分方法,那么所有可能的分箱数 $2^k-2$ 就会超过最大值maxBins了,这时就采用称之为排序切分的方法,将每个可能的取值看成一个分箱,例如一个人的年龄阶层可能有5种情况“老中青少幼”,那个所有可能的分箱数为5种,分别是:“老”、“中”、“青”、“少”、“幼”,所有可能的切分方案为4种(分箱数-1),具体按照什么顺序切分,mllib中按分箱内所有实例的不确定性顺序进行切分,例如上述5个分箱内的样本不确定性(基尼系数或是方差)从小到大为“老”、“中”、“青”、“少”、“幼”,那么可能的切分方案为:“老 | 中青少幼”、“老中 | 青少幼”、“老中青 | 少幼”、“老中青少 | 幼”,这种排序切分方案适用于二分类和回归问题。
continuous feature 切分
如果特征是 continuous feature(参数categoricalFeaturesInfo指定以外的特征),那么首先就需要离散化,将连续的特征值划分到不同的分箱(bin)里去,分箱代表一个区间,一个实例的对应特征值在区间里的表示属于那个分箱,mllib采用的分位点排序策略,首先对所有训练数据进行采样,得到部分样本实例,假如其对应的某个特征值分别为0.1, 0.11, 0.2, 0.11, 0.6, 0.3, 0.22,对特征值进行排序得到0.1, 0.11, 0.11, 0.2, 0.22, 0.3, 0.6,如果参数maxBins设置为3,那么理论上平均每个分箱的实例数为样本实例数/numBin,即7/3=2.33,从左到右进行扫描,得到分箱为 $(-\infty, 0.2),[0.2, 0.3),[0.3, \infty)$ ,对应的所有切分方案(上界)为2种,分别为0.2, 0.3。
最优切分点与树的形成
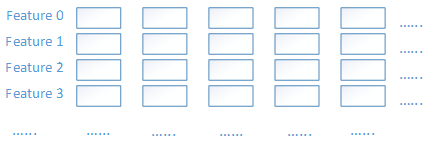
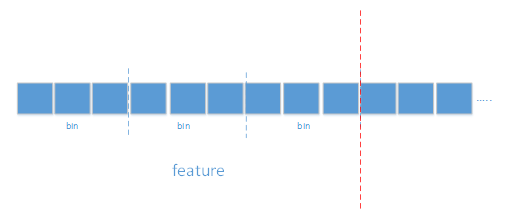
经过上述分箱划分后,每个特征都对应一组分箱bins,如下图所示,根据分箱情况,将实例的所有特征映射到其对应的分箱中,每个分箱就包含一组实例,得到一些统计信息,用于计算不确定性。
对于分类树,假设不确定性指标为基尼系数gini,则每个bin的统计信息包含:1)每个类别对应的实例数 $C_i$ ;2)该bin的实例总和 $C$ 。那么可以根据以下公式求得基尼系数为:
$$ gini = \sum_{i}^K \frac {C_i} {C} (1 - \frac {C_i} {C}) $$
对于回归树,其不确定性指标为方差variance,则每个bin的统计信息包含:1)该bin的所有实例总和C;2)该bin所有实例的lebel总和 $\sum y_i$ ;3)该bin所有实例的lebel平方和 $\sum {y_i}^2$ 。那么可以根据以下公式(其中u为均值)求得方差为:
$$ variance = \frac {1} {C} \sum {(y_i - u)}^2 = \frac {1} {C} (\sum {y_i}^2 - \frac {1} {C} {(\sum {y_i})}^2) $$
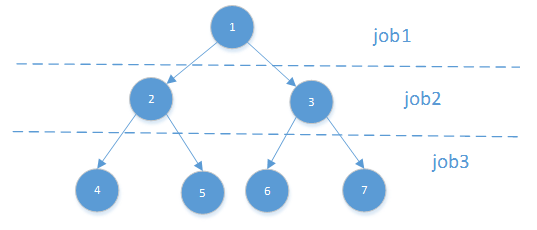
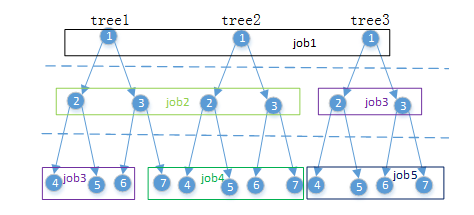
Mllib在生成决策树的过程中,是按照树的层次一步步迭代,每一次对处于同一层的节点进行划分,相应地会触发一个job,如果树的深度为N,那么至少需要跑N个job才能训练得到一棵树,如下图所示。
假设已经迭代到上图中的job2,首先会为每个要切分的节点初始化一个DTStatsAggregator对象,DTStatsAggregator封装了所有特征分箱的统计信息,这些统计信息用于计算分箱的不确定性,下图显示一次迭代计算最优切分点的过程。
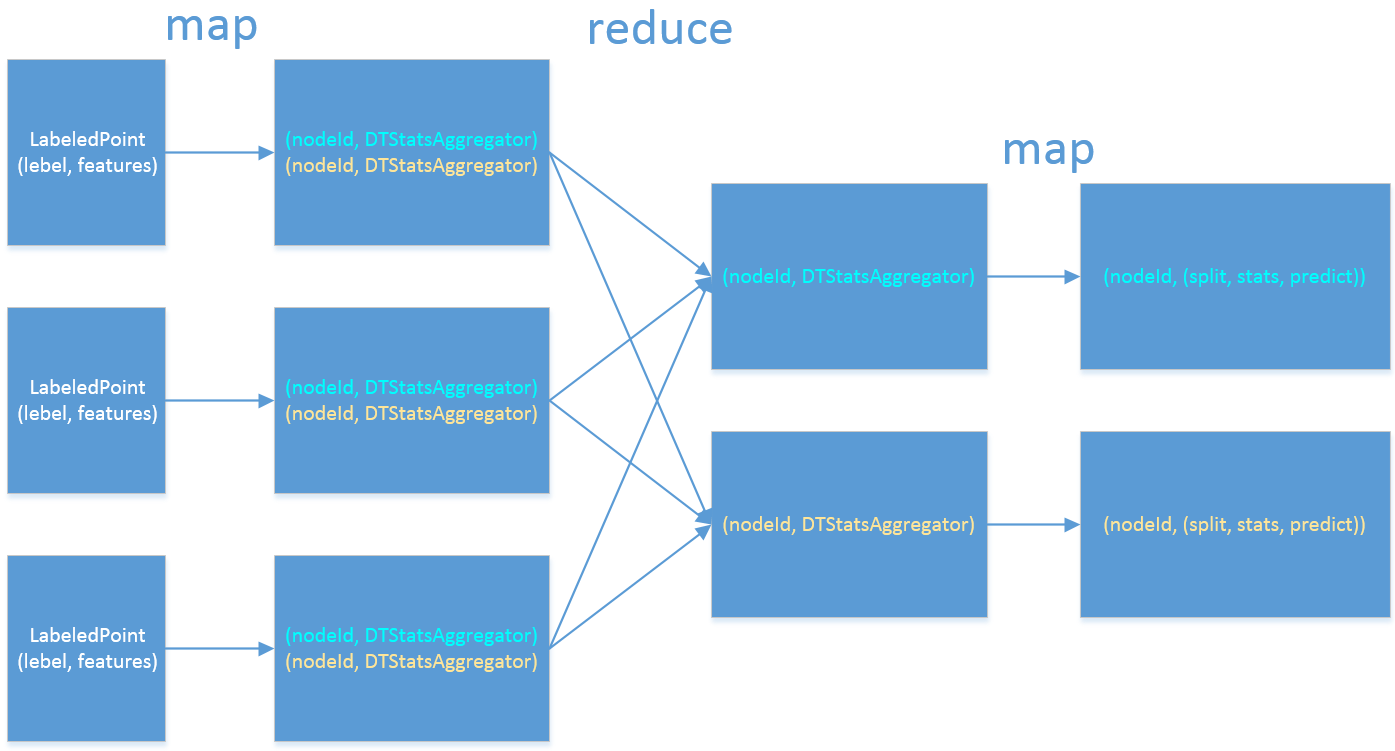
如上图,首先在每个partition上做一次map,遍历该partition上的所有实例,根据前面的分箱情况,将实例映射到分箱中,并更新分箱的统计信息, map操作后得到记录是(nodeId, DTStatsAggregator),其中nodeId表示节点id,即需要对哪个节点进行切分,DTStatsAggregator对象保存了所有特征所有分箱的统计信息,然后再根据nodeId做一次reduce,将不同分区的分箱统计信息归并起来,最终得到不同节点(nodeId)上所有样本的分箱统计信息(nodeId, DTStatsAggregator),最后再做一次map,对于每个节点,遍历所有可能的切分方案,找到不确定性减少最多的切分方案,即最优切分点。DTStatsAggregator对象中维护了一个大数组,该数组保存了所有特征的分箱统计信息,如下图所示,某个特征有3个bin,每个bin的统计信息由前面所述3个计算方差的统计值组成。
如何根据bin的统计信息遍历所有可能的切分方案呢?再看看前面讨论的特征划分,在初始化介绍后,我们是知道每个特征的所有可能的划分方案的,不同特征的划分也做了详细的区分。假如上图中feature是 continuous feature,那么3个bin对应2种切分方案,遍历这两种切分方案,得到切分后不确定减小的较多的切分方案,类似地,遍历所有特征的所有切分可能,最后得到一个最优切分点。
集成树
集成树 Ensemble Tree 是综合多个决策树以得到更加泛化的模型,这样可以消除噪声,避免过拟合。常见的集成树有随机森林(Random Forests)和梯度提升树(Gradient-Boosted Tree),下面分别详细介绍。
随机森林
随机森林(Random Forests)其实就是多个决策树,每个决策树有一个权重,对未知数据进行预测时,会用多个决策树分别预测一个值,然后考虑树的权重,将这多个预测值综合起来,对于分类问题,采用多数表决,对于回归问题,直接求平均。
随机森林模型训练实质上是同时训练多个决策树,每个决策树的训练样本是从原始训练集中抽样而来。在具体训练模型时,mllib做了一个优化,是同时对多个决策树进行训练,如下图所示,每个job会对一组节点进行切分,分组是按照树的层次逐步进行,每组需要切分的节点个数视内存大小而定,有一个参数maxMemoryInMB控制一次切分计算使用的最大内存大小,通过简单的估计节点切分计算所需内存(主要是计算分箱统计信息占用内存的大小)来决定一组节点的个数。
梯度提升树
梯度提升树(Gradient-Boosted Tree)简称GBT,是一种更加复杂的模型,它实质上是采用Boost方法,利用基本决策树模型得到的一种集成树模型。GBT的训练是每次训练一颗树,然后利用这颗树对每个实例进行预测,通过一个损失函数,计算损失函数的负梯度值作为残差,利用这个残差更新样本实例的label,然后再次训练一颗树去拟合残差,如此进行迭代,直到满足模型参数需求。GBT只适用于二分类和回归,不支持多分类,在预测的时候,不像随机森林那样求平均值,GBT是将所有树的预测值相加求和。
转载请注明出处,本文永久链接:https://sharkdtu.github.io/posts/mllib-tree.html

